Getaran bebas tanpa peredam
Pada model yang paling sederhana redaman dianggap dapat diabaikan, dan tidak ada gaya luar yang memengaruhi massa (getaran bebas).Dalam keadaan ini gaya yang berlaku pada pegas Fs sebanding dengan panjang pereganganx, sesuai dengan hukum Hooke, atau bila dirumuskan secara matematis:
Sesuai Hukum kedua Newton gaya yang ditimbulkan sebanding dengan percepatan massa:
Bila massa dan kekakuan (tetapan k) diketahui frekuensi getaran sistem akan dapat ditentukan menggunakan rumus di atas.
[sunting] Getaran bebas dengan redaman
Bila peredaman diperhitungkan, berarti gaya peredam juga berlaku pada massa selain gaya yang disebabkan oleh peregangan pegas. Bila bergerak dalam fluida benda akan mendapatkan peredaman karena kekentalan fluida. Gaya akibat kekentalan ini sebanding dengan kecepatan benda. Konstanta akibat kekentalan (viskositas) c ini dinamakan koefisien peredam, dengan satuan N s/m (SI)Nilai koefisien redaman yang diperlukan untuk mencapai titik redaman kritis pada model massa-pegas-peredam adalah:
Solusi sistem kurang redam pada model massa-pegas-peredam adalah
Nilai X, amplitudo awal, dan φ, ingsutan fase, ditentukan oleh panjang regangan pegas.
Dari solusi tersebut perlu diperhatikan dua hal: faktor eksponensial dan fungsi cosinus. Faktor eksponensial menentukan seberapa cepat sistem teredam: semakin besar nisbah redaman, semakin cepat sistem teredam ke titik nol. Fungsi kosinus melambangkan osilasi sistem, namun frekuensi osilasi berbeda daripada kasus tidak teredam.
Frekuensi dalam hal ini disebut "frekuensi alamiah teredam", fd, dan terhubung dengan frekuensi alamiah takredam lewat rumus berikut.



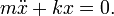

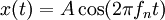
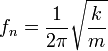

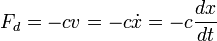




Tidak ada komentar:
Posting Komentar